|
Peak
to average power ratio reduction of OFDM signals using
Peak Reduction Carriers
|
E.
Lawrey, C. J. Kikkert
Electrical and Computer Engineering
James Cook University, Douglas Campus, Townsville, Queensland,
4814, Australia
Email: ofdm@skydsp.com,
Keith.Kikkert@jcu.edu.au |
Published: Fifth
International Symposium on Signal Processing and its
Applications,
ISSPA ’99, Brisbane, Australia, 22-25 August, 1999
Organised by the Signal Processing Research Centre,
QUT,
Brisbane, Australia
|
Abstract
A technique is described for a better than 5 dB reduction in
the Peak to Average Power Ratio (PAPR) of an OFDM signal. The
optimal amplitude and phase of additional peak reduction carriers
(PRC) is obtained using a code-book, which is obtained using
a search of all possible signal combinations.
1 Introduction
Wireless digital communications is rapidly expanding, resulting
in a demand for wireless systems that are reliable and have
a high spectral efficiency. Orthogonal Frequency Division Multiplexing
(OFDM) has a high tolerance to multipath signals and is spectrally
efficient making it a good candidate for future wireless communication
systems.
One disadvantage of OFDM is that the peak of the signal can
be up to N times the average power (where N is the number
of carriers). These large peaks increase the amount of intermodulation
distortion resulting in an increase in the error rate. The
average signal power must be kept low in order to prevent
the transmitter amplifier limiting. Minimising the PAPR allows
a higher average power to be transmitted for a fixed peak
power, improving the overall signal to noise ratio at the
receiver. It is therefore important to minimise the PAPR.
A large amount of research has been done on broadcast OFDM
systems, however most wireless communication systems must
support multiple users. One application that a multi-user
OFDM system would be suitable for is fixed wireless telephony
applications. In such a system each user is allocated a small
percentage of the system carriers, typically 4-16 depending
on the symbol rate used. This paper presents a method for
reducing the PAPR of a OFDM signal that contains data. It
is optimised for a low number of carriers making it a suitable
technique for multi-user OFDM.
2 Background
The PAPR of an OFDM signal can be reduced in several ways. Selective
mapping [1, 2] involves generating a large set of data vectors
all representing the same information. The data vector with
the lowest resulting PAPR is selected. Information about which
particular data vector was used is sent as additional carriers.
However there may be potential problems with decoding the signal
in the presence of noise with selective mapping. Errors in the
reverse mapping would result in the data of whole symbols being
lost.
Another technique similar to selective mapping is using Golay
sequences [6]. Information is transmitted by mapping each
data word with a Golay sequence. Using Golay sequences result
in a low PAPR, typically 3-6 dB, however the coding rate is
poor, typically half, resulting in a large bandwidth increase.
Cyclic coding [3] involves adding extra carriers in which
the phase of every fourth carrier is calculated based on an
algorithm using the phase of the previous three information
carriers. This method is similar to the presented technique
except that it gives sub optimal results.
3 Peak Reduction Carriers
This paper presents a technique that combines selective mapping
and cyclic coding. A reduction in the PAPR is achieved by adding
extra carriers referred to as Peak Reduction Carriers (PRC).
The phase and amplitude of the PRCs is varied to minimise the
overall PAPR. The original information carriers are unaffected
and can be decoded normally. The receiver can disregard the
PRCs, or they can be used for error detection. The frequency
of PRCs, or relative positioning of the PRCs can be varied with
respect to the information carriers depending on the application.
The results presented were found using a computationally intensive
exhaustive search to find the optimal setting for the PRCs.
However it is assumed that further work will allow a more efficient
algorithm to be found.
An optimal setting for the PRCs corresponds to the combination
of phase and amplitude that achieves the lowest PAPR of the
overall OFDM symbol (information carriers and PRCs). In this
paper the phase and amplitude of the PRCs was set in a coarse
quantised manner to minimise the number of combinations needed
to be searched. The phase of the PRCs was set to 0° or
180° and the carriers were turned on or off. There are
therefore 3M combinations for the PRCs for each
information code word (where M is the number of PRCs). This
level of quantisation was found to be appropriate for BPSK
information carriers. Finer quantisation may produce improved
results for higher modulation schemes.
An exhaustive search of all combinations of allowable phase
and amplitude gives optimal PRCs, but is computationally intensive.
This method can be used for small numbers of carriers where
the optimal PRC coding can be stored in a look up table or
code-book. This is impractical for more than 16 information
carriers or for more than 10 PRCs as the number of combinations
becomes too large to store and calculate. However for some
multi-user OFDM applications 16 or less carriers per user
is sufficient.
The results shown were calculated based on all combinations
of information code words, thus will give a good indication
of the practical PAPR improvement.
For each experiment the inverse fast Fourier transform (IFFT)
of the carrier configuration was used to give a complex base
band signal. Let the complex base band signal be defined as
in eqn. 1.
|
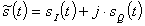
|
(1)
|
When this is quadrature modulated to RF the signal can be written
in polar form as:
|
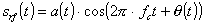
|
(2)
|
where a(t) is the amplitude and q(t) is the phase of the signal.
Thus:
|
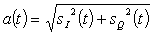
|
(3)
|
The definition of the PAPR in eqn 4, where T is the OFDM symbol
period, can be used for RF as well as base band [1].
|
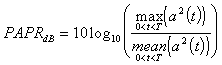
|
(4)
|
For the simulations carried out, the base band carriers were
centred on DC and the size of the IFFT was made at least 8 times
greater than the number of carriers, oversampling the time domain
signal. This ensures that peaks in the signal were accurately
represented to get an accurate PAPR [4, 5].
3.1 Results
The simplest arrangement for the relative positioning of
the data and PRCs is to have a block of data carriers immediately
followed by a block of PRCs. This arrangement was used for
the results shown in figures 1-3.
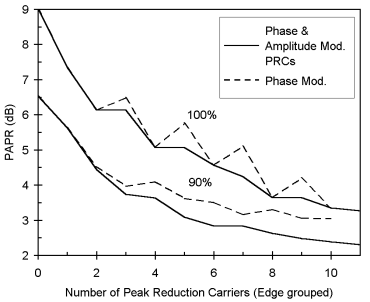
Figure 1. PAPR verses number of edge grouped
PRCs (8 BPSK data carriers)
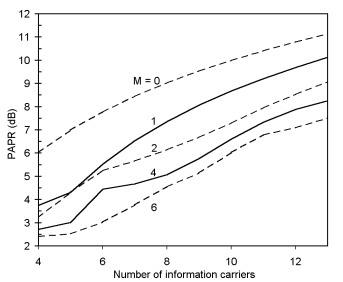
Figure 2. Maximum PAPR verses number of data
carriers and edge grouped PRCs, where M is the number of
PRCs.
Figure 1 shows the worst case PAPR and the 90% point in the
cumulative distribution of PAPR as the number of PRCs is increased.
The maximum PAPR for the 8 information carriers is reduced
by >5.5dB for the addition of 10 PRCs. Selecting the optimal
amplitude and phase of the PRC improves the performance significantly
as compared with only setting the phase as used in cyclic
coding [3]. For this reason phase and amplitude modulation
of the PRCs was used in all later experiments due to the improved
performance.
Figure 2 shows the effect of adding PRCs to the PAPR as the
number of information carriers is varied. The improvement
in PAPR remains relatively constant as the number of information
carriers is increased. This shows that this technique gives
consistent performance gains as the number of information
carriers is varied.
Adding PRCs reduces the PAPR at the expense of additional
transmission power. Figure 3 shows the net improvement in
PAPR due to the addition of PRCs. The PAPR reduction was calculated
as the difference between the PAPR results for zero PRCs and
the PAPR results with the addition of PRCs. The loss in signal
power due to the PRCs was then subtracted from the PAPR reduction
in order to give the net PAPR improvement. If the data signal
power lost due to the transmission of the PRCs was more than
the PAPR gain then there would be little point in adding the
PRCs. It can be seen that for 10 BPSK carriers there is little
improvement in adding more than 2 PRCs. In fact adding more
than 5 PRCs results in a worsening of the average (50%) PAPR.
This is due to the power cost of the PRCs.
4 Effect of PRC Position
Previous results are shown for grouped PRCs that were positioned
immediately after the data carriers as shown in Figure 4a. Two
different positioning tests were performed. One test kept the
PRCs grouped together as in Figure 4a, however they were moved
with respect to the data carriers as in Figure 4b.The second
test positioned the PRCs in a spread out manner. The best spread
pattern was established using a randomised search.
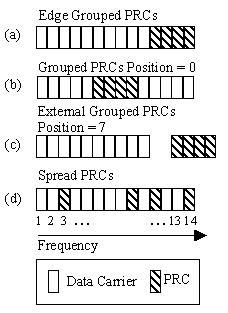
Figure 4. PRC position combinations
|
Adding PRCs use a significant amount of additional bandwidth.
It is therefore important to minimise the number used, or to
position the PRCs so that the bandwidth can be reused. For example,
in a multi-user OFDM system where each user transmits a block
of carriers, the PRCs can be overlapped, i.e. they are transmitted
at the same frequency, effectively halving the bandwidth.
4.1 Grouped PRCs
In this scheme the PRCs were maintained as a group of carriers.
They were repositioned by sliding them with respect to the
data carriers. Figure 5 and 6 show the effect of the position
on effectiveness of the PRCs. Figure 5 shows for a small number
of PRCs the position of the PRCs within the data carriers
has little effect on the performance. However with 4 or more
PRCs the position has a significant effect on the performance
of the PRCs.Placing the PRCs within the data carriers with
an off centre of 3 carriers gives the best results. This gives
a further reduction of 1dB as compared with edge grouped PRCs.
Not having edge grouped PRCs would prevent overlapping of
the PRCs for a multi-user OFDM, thus doubling the bandwidth
used by the PRCs.
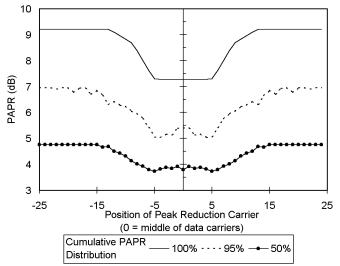
Figure 5. PAPR verses position of 2 grouped PRCs
(10 BPSK data carriers)
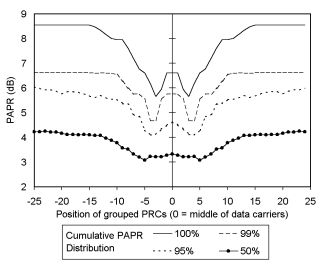
Figure 6. PAPR verses position of 4 grouped PRCs
(10 BPSK data carriers)
4.2 Spread PRCs
The position of the 4 grouped PRCs had a significant effect
on the PRC performance, thus it seemed likely that spreading
the PRCs out might lead to further improvements. The exact relationship
between the position of the PRCs and the PAPR distribution is
currently unknown and so a random search was used for optimisation.
The PRCs and data carriers were positioned randomly to form
a block of carriers with no gaps as shown in figure 4d. For
each position combination the PAPR distribution was found and
the combination which resulted in the lowest maximum PAPR was
selected as the optimised PRCs position.
The PAPR distribution was found by testing all
combinations of the data code words. For each data code word
combination the optimum PRCs were found as described in section
3. The PAPR distribution verses the number of PRCs is shown
in figure 7. This result is for 10 data carriers and shows
that spreading the PRCs can result in large reductions in
the PAPR of the OFDM symbol. A reduction of > 6dB is possible.
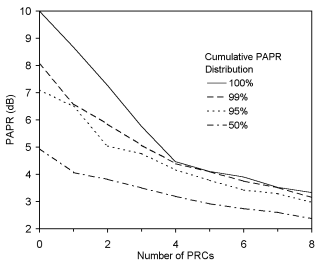
Figure 7. PAPR verses the number of spread PRCs
(10 BPSK data carriers)
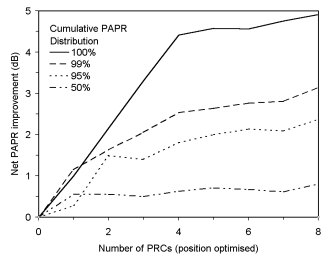
Figure 8. Net improvement in PAPR, position optimised
PRCs (10 BPSK data carriers)
Figure 8 shows the overall net improvement in the PAPR using
position optimised PRC. This can be directly compared to figure
3 which shows the results for edge grouped PRCs. The maximum
net gain for position optimised PRCs is nearly double that
of the edge grouped PRCs. Figure 8 shows that the net PAPR
gain increases rapidly up to 4 PRCs, after which the gain
is minimal. Thus the optimal number of PRCs would be 4 for
10 data carriers. Other tests also show that the number of
PRCs needs to be approximately 40% of the number of data carriers
in order to get significant improvements in the PAPR.
Overlapping of the spread PRCs in a multi-user OFDM system
is more difficult as most of the PRCs will be bounded with
data carriers. Thus simple overlapping may not be possible.
This would be the case if the data and PRC are grouped. However
if the carriers for each user are spread out it might be possible
have spread out PRCs that overlap between the users, but still
provide a large reduction in the PAPR.
The addition of 4 PRCs with 10 data carriers results is a
large net gain of 4.5 dB, allowing more power to be transmitted.
For a transmission with no PRCs at an error rate of 1x10-3,
adding the PRCs and maintaining the same peak power the error
rate would be decreased to 1x10-7 [7]. This is
more efficient than adding error correcting bits at the same
coding rate. For example using Hamming coding at a rate of
4 parity bits for 11 data bits gives a gain of only 1.2 dB
at a bit error rate of 1x10-4 [7] which is significantly
less than 4.5dB.
Table 1 shows the number PRC positions tested, and the best
combination found.
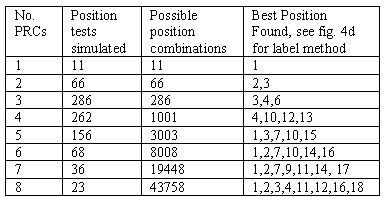
Table 1. Optimised positions found for
10 BPSK data carriers |
5 Conclusion
Adding peak reduction carriers can significantly improve the
PAPR of an OFDM signal. The PRCs can result in a reduction of
>6dB in the maximum PAPR and a net reduction of >4.5dB when
the additional power for PRCs is taken into account. It was
found that varying the amplitude as well as phase for the PRCs
gave improved performance over just phase variation. It was
also found that spreading the position of the PRCs resulted
in a better performance than grouped PRCs. Adding more PRCs
results in a lower PAPR, however the use of large numbers of
PRCs is limited by the cost of additional transmission power,
bandwidth and complexity limits.
6 References
1. Bauml, R.W., Fischer, R.F.H., Huber, J.B., Reducing the
peak-to-average power ratio of multicarrier modulation by selected
mapping, Electronic Letters, 1996, Vol. 32, pp. 2056-2057
2. Van Eetvelt, J., Wade, G., Tomlinson, M., Peak to average
power reduction for OFDM schemes by selective scrambling,
Electronic Letters, 1996, Vol. 32, pp. 1963-1964
3. Wulich, D., Reduction of peak to mean ratio of
multicarrier modulation using cyclic coding, Electronic
Letters, 1996, Vol. 32, pp. 432-433
4. Tellambura, C., Use of m-sequences for OFDM peak-to-average
power ratio reduction, Electronic. Letters, 1997, Vol.
33, pp. 1300-1301
5. Tellambura, C., Phase optimisation criterion
for reducing peak-to-average power ratio in OFDM, Electronic
Letters, 1998, Vol. 34, pp. 169-170
6. Davis, J.A., Jedwab, J., Peak-to-mean power control
and error correction for OFDM transmission using Golay sequences
and Reed-Muller codes, Electronic Letters, 1997, Vol.
33, pp. 267-268
7. Sklar, B., Digital Communications Fundamentals and
Applications, Prentice Hall, 1988, pp. 300
|


